Чему равна 3 космическая скорость – Третья космическая скорость — Википедия

Третья космическая скорость — Википедия

Материал из Википедии — свободной энциклопедии

Тре́тья косми́ческая ско́рость — минимальная скорость, которую необходимо придать находящемуся вблизи поверхности Земли телу, чтобы оно могло преодолеть гравитационное притяжение Земли и Солнца и покинуть пределы Солнечной системы^[1].

Для того, чтобы покинуть пределы Солнечной системы с орбиты Земли, ракета массой m{\displaystyle m} должна обладать скоростью относительно Солнца vC{\displaystyle v_{C}}, определяемой законом сохранения энергии

mvC22=GmMCRZC,{\displaystyle {\frac {mv_{C}^{2}}{2}}=G{\frac {mM_{C}}{R_{ZC}}},}

где MC{\displaystyle M_{C}} — масса Солнца, RZC{\displaystyle R_{ZC}} — радиус земной орбиты. Отсюда требуемая скорость ракеты относительно Солнца

vC=2GMCRZC.{\displaystyle v_{C}={\sqrt {\frac {2GM_{C}}{R_{ZC}}}}.}

Ракета вследствие движения вместе с Землей по орбите вокруг Солнца уже обладает скоростью вращения Земли вокруг Солнца, которую можно найти, применив второй закон Ньютона:

GMCmRZC2=mvZ2RZC,{\displaystyle G{\frac {M_{C}m}{R_{ZC}^{2}}}={\frac {mv_{Z}^{2}}{R_{ZC}}},}

откуда

vZ=GMCRZC.{\displaystyle v_{Z}={\sqrt {\frac {GM_{C}}{R_{ZC}}}}.}

Следовательно, при разгоне ракеты в направлении вектора скорости движения Земли по её орбите вокруг Солнца скорость космической ракеты vRZ{\displaystyle v_{RZ}} относительно Земли для выхода за пределы Солнечной системы должна быть равна

vRZ=vC−vZ=vZ(2−1).{\displaystyle v_{RZ}=v_{C}-v_{Z}=v_{Z}({\sqrt {2}}-1).}

Для того, чтобы удалить корабль из поля тяготения Земли, ему надо сообщить вторую космическую скорость

v2=2GMZRZ.{\displaystyle v_{2}={\sqrt {\frac {2GM_{Z}}{R_{Z}}}}.}

Следовательно, кинетическая энергия Ek{\displaystyle E_{k}}, которую надо сообщить космическому кораблю для того, чтобы он покинул Солнечную систему, складывается из кинетической энергии E2{\displaystyle E_{2}}, необходимой для того, чтобы покинуть поле тяготения Земли и кинетической энергии ERZ{\displaystyle E_{RZ}}, необходимой для того, чтобы он с орбиты Земли покинул поле тяготения Солнца

mv322=mv222+mvRZ22,{\displaystyle {\frac {mv_{3}^{2}}{2}}={\frac {mv_{2}^{2}}{2}}+{\frac {mv_{RZ}^{2}}{2}},}

откуда v3=v22+vRZ2{\displaystyle v_{3}={\sqrt {v_{2}^{2}+v_{RZ}^{2}}}}^[2].

Отсюда приходим к формуле^[3]:

v3=(2−1)2vZ2+v22,{\displaystyle v_{3}={\sqrt {({\sqrt {2}}-1)^{2}v_{Z}^{2}+v_{2}^{2}}},}

где vZ{\displaystyle v_{Z}} — орбитальная скорость планеты, v2{\displaystyle v_{2}} — вторая космическая скорость для планеты.

Подставляя численные значения (для Земли vZ{\displaystyle v_{Z}} = 29,783 км/с, v2{\displaystyle v_{2}} = 11,182 км/с), найдём

v3≈{\displaystyle v_{3}\approx } 16,650 км/с.

При старте с Земли, наилучшим образом используя осевое вращение (≈0,5 км/с) и орбитальное движение планеты (≈29,8 км/с), космический аппарат может достичь третьей космической скорости уже при ~16,6 км/с^[1] относительно Земли. Для исключения влияния атмосферного сопротивления предполагается, что космический аппарат приобретает эту скорость за пределами атмосферы Земли. Наиболее энергетически выгодный старт для достижения третьей космической скорости должен осуществляться вблизи экватора, движение объекта должно быть сонаправлено осевому вращению Земли и орбитальному движению Земли вокруг Солнца. При этом скорость движения аппарата относительно Солнца составит

29,8 + 16,6 + 0,5 = 46,9 км/с.

Траектория аппарата, достигшего третьей космической скорости, будет частью ветви параболы, а скорость относительно Солнца будет асимптотически стремиться к нулю.

На начало 2015 г. ни один космический аппарат не покидал окрестностей Земли с третьей космической скоростью. Наибольшей скоростью покидания Земли обладал КА Новые горизонты; эта скорость составила 16,26 км/с^[4] (гелиоцентрическая скорость 45 км/с), что меньше третьей космической на 0.34 км/с. Но за счёт гравитационного манёвра у Юпитера в 2007 году он ещё прибавил 4 км/c, что позволит ему в будущем уверенно покинуть гелиосферу. На момент окончания основной части своей миссии (исследование Плутона) «Новые горизонты» удалялись от Солнца с гелиоцентрической скоростью около 14 км/с ^{[источник не указан 1838 дней]}. Аналогичным образом ускорялись и другие КА, уже покинувшие гелиосферу (Вояджер-1, Вояджер-2, Пионер-10 и Пионер-11). Все они покидали окрестности Земли со скоростями, существенно меньшими третьей космической.

1. ↑ ^{1 2} Третья космическая скорость // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
2. ↑ Кабардин О. Ф., Орлов В. А. Пономарева А. В. Факультативный курс физики. 8 класс. — М.: Просвещение, 1985 — с. 178
3. ↑ Галузо И. В. Астрономия : учеб. пособие для 11-го кл. общеобразоват. учреждений с рус. яз. обучения / И. В. Галузо, В. А. Голубев, А. А. Шимбалёв. — 2-е изд., пересмотр. — Минск: Нар. асвета, 2009. — С. 70. — ISBN 978-985-03-1083-5.
4. ↑ New Horizons Mission to Pluto — Windows to the Universe

ru.wikipedia.org

Третья космическая скорость

   Третья космическая скорость — минимальная скорость, которую необходимо придать находящемуся вблизи поверхности Земли телу, чтобы оно могло преодолеть гравитационное притяжение Земли и Солнца и покинуть пределы Солнечной системы.

где v₃ — третья космическая скорость, а v₁ и v₂ — первая для Солнца и вторая для планеты космические скорости соответственно.

Полезная информация о третьей космической скорости:

   У поверхности Земли третья космическая скорость равна 16,7 км/с.

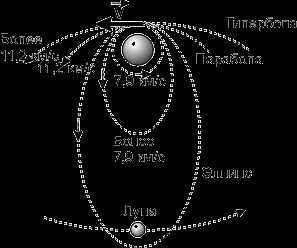
   При начальной скорости больше 7,9 км/с, но меньше 11,2 км/с космический аппарат движется вокруг Земли по криволинейной траектории — эллипсу. Чем больше начальная скорость, тем все более вытянут эллипс.

   При достижении некоторого значения скорости, называемого второй космической скоростью, эллипс превращается в параболу и космический корабль уходит от Земли безвозвратно. У поверхности Земли вторая космическая скорость равна 11,2 км/с. При скорости более второй космической тело движется по гиперболической траектории.

   При старте с Земли, наилучшим образом используя осевое вращение (≈0,5 км/с) и орбитальное движение планеты (≈29,8 км/с), космический аппарат может достичь третьей космической скорости уже при ~16,6 км/с относительно Земли. Для исключения влияния атмосферного сопротивления предполагается, что космический аппарат приобретает эту скорость за пределами атмосферы Земли. Наиболее энергетически выгодный старт для достижения третьей космической скорости должен осуществляться вблизи экватора, движение объекта должно быть сонаправлено осевому вращению Земли и орбитальному движению Земли вокруг Солнца. При этом скорость движения аппарата относительно Солнца составит 29,8 + 16,6 + 0,5 = 46,9 км/с.

   Траектория аппарата, достигшего третьей космической скорости, будет частью ветви параболы, а скорость относительно Солнца будет асимптотически стремиться к нулю.

   На 2012 год ещё ни один космический аппарат не покидал окрестностей Земли с третьей космической скоростью. Наибольшей скоростью покидания Земли обладал космический аппарат Новые горизонты — 16,21 км/с, но за счёт гравитационного маневра у Юпитера, он покинет Солнечную систему со скоростью около 30 км/с после окончания основной части своей миссии. Аналогичным образом ускорялись и другие космические аппараты, уже покинувшие Солнечную систему (Вояджер-1, Вояджер-2, Пионер-10 и Пионер-11). Все они покидали окрестности Земли со скоростями, существенно меньшими третьей космической.

Так же есть:

Первая космическая скорость: 

Вторая космическая скорость :   

Обозначения:

 — Первая космическая скорость

 — Вторая космическая скорость

 — Гравитационная постоянная

 — Масса Земли

 — Радиус Земли

 — Высота тела над поверхностью Земли

g — Ускорение свободного падения у поверхности Земли

infofiz.ru

Космическая скорость — Википедия

Материал из Википедии — свободной энциклопедии

Косми́ческие ско́рости (первая v₁, вторая v₂, третья v₃ и четвёртая v₄^[1]) — характерные критические скорости движения космических объектов в гравитационных полях небесных тел и их систем. Космические скорости используются для характеристики типа движения космического аппарата в сфере действия небесных тел: Солнца, Земли и Луны, других планет и их естественных спутников, а также астероидов и комет.

По определению, космическая скорость — это минимальная начальная скорость, которую необходимо придать объекту (например, космическому аппарату) на поверхности небесного тела в отсутствие атмосферы, чтобы:

• v₁ — объект стал искусственным спутником центрального тела, то есть стал вращаться по круговой орбите вокруг него на нулевой или пренебрежимо малой высоте относительно поверхности;
• v₂ — объект преодолел гравитационное притяжение центрального тела и начал двигаться по параболической орбите, получив тем самым возможность удалиться на бесконечно большое расстояние от него;
• v₃ — при запуске с планеты объект покинул планетную систему, преодолев притяжение звезды, то есть это параболическая скорость относительно звезды;
• v₄ — при запуске из планетной системы объект покинул галактику.

Космические скорости могут быть рассчитаны для любого удаления от центра Земли. Однако в космонавтике часто используются величины, рассчитанные конкретно для поверхности шаровой однородной модели Земли радиусом 6371 км.

Квадрат круговой (первой космической) скорости с точностью до знака равен ньютоновскому потенциалу Φ на поверхности небесного тела (при выборе нулевого потенциала на бесконечности):

v12=−Φ=GMR,{\displaystyle v_{1}^{2}=-\Phi ={\frac {GM}{R}},}

где M — масса небесного тела, R — его радиус, G — гравитационная постоянная.

Если скорость КА или другого объекта в момент вывода на орбиту превышает круговую, его орбитой будет эллипс с фокусом в центре притяжения.

Между первой и второй космическими скоростями в нерелятивистском случае существует простое соотношение:

v2=2⋅v1.{\displaystyle v_{2}={\sqrt {2}}\cdot v_{1}.}

Квадрат скорости убегания (второй космической скорости) равен удвоенному ньютоновскому потенциалу на поверхности тела, взятому с обратным знаком:

v22=−2Φ=2GMR.{\displaystyle v_{2}^{2}=-2\Phi =2{\frac {GM}{R}}.}

Вторая космическая скорость (параболическая скорость, скорость убегания) обычно определяется в предположении отсутствия каких-либо других небесных тел. Например, для Луны скорость убегания равна 2,4 км/с, несмотря на то, что в действительности для удаления тела на бесконечность с поверхности Луны необходимо преодолеть притяжение Земли, Солнца и Галактики.

Первая и вторая космические скорости для различных небесных тел[править | править код]

Небесное тело	Масса (по отношению к массе Земли)[2]	v1, км/с[3]	v2, км/с[4]
Энцелад	1,8×10−5[5]	0,169	0,239[6]
Церера	1,57×10−4[7]	1,678	2,4[6]
Луна	0,0123	1,678	2,4
Меркурий	0,0553	3,005	4,3
Венера	0,815	7,325	10,4
Земля	1	7,91	11,2
Марс	0,107	3,546	5,0
Юпитер	317,8	42,58	59,5
Сатурн	95,2	25,535	35,5
Уран	14,54	15,121	21,3
Нептун	17,1	16,666	23,5
Солнце	332 940	437,047	618,1[6]
Ближайший белый карлик Сириус B	338 933	4 800	6 800[6]
Нейтронная звезда PSR J0348+0432[en]	ок. 670 000	143 000 ± 10 000[8]	~ 200 000[8][6]

КА, начальная скорость которого не меньше третьей космической скорости, в состоянии преодолеть притяжение Солнца и навсегда покинуть пределы Солнечной системы. Только на космических кораблях, которым доступны такие скорости, принципиально могут быть осуществлены пилотируемые межзвёздные перелёты к планетным системам других звёзд.

Четвёртая и пятая космическая скорости[править | править код]

Четвёртая космическая скорость используется довольно редко.

Ещё реже в некоторых источниках встречается понятие «пятая космическая скорость». Это скорость, позволяющая добраться до иной планеты звездной системы вне зависимости от разности плоскостей эклиптики планет. Например, для Солнечной системы и, конкретно, для Земли, чтобы орбита межпланетного перелета была перпендикулярной к земной орбите, нужна скорость запуска 43,6 километра в секунду^[9]

1. ↑ Засов А. В., Сурдин В. Г. Космические скорости.
2. ↑ Dr. David R. Williams. Planetary Fact Sheet — Ratio to Earth Values (англ.). NASA. Дата обращения 16 ноября 2017.
3. ↑ Первая космическая скорость, онлайн расчет (неопр.). Калькулятор – справочный портал. Дата обращения 26 июля 2019.
4. ↑ Dr. David R. Williams. Planetary Fact Sheet — Metric (англ.). NASA. Дата обращения 16 ноября 2017.
5. ↑ Jacobson, R. A.; Antreasian, P. G.; Bordi, J. J.; Criddle, K. E. et al. The Gravity Field of the Saturnian System from Satellite Observations and Spacecraft Tracking Data (англ.) // The Astronomical Journal : journal. — IOP Publishing, 2006. — December (vol. 132). — P. 2520—2526. — DOI:10.1086/508812.
6. ↑ ^{1 2 3 4 5} Вторая космическая скорость, онлайн расчет (неопр.). Калькулятор – справочный портал. Дата обращения 28 июля 2019.
7. ↑ Carry, Benoit; et al. Near-Infrared Mapping and Physical Properties of the Dwarf-Planet Ceres (англ.) // Astronomy and Astrophysics : journal. — EDP Sciences, 2007. — November (vol. 478). — P. 235—244. — DOI:10.1051/0004-6361:20078166. (недоступная ссылка)
8. ↑ ^{1 2} Строго говоря, при расчёте должны учитываться релятивистские поправки, однако гораздо большую неточность вносит имеющая место на сегодняшний день неопределённость значения радиуса нейтронной звезды
9. ↑ Анатолий Шибанов. Заботы космического архитектора

ru.wikipedia.org

Третья космическая скорость — это… Что такое Третья космическая скорость?

Тре́тья косми́ческая ско́рость — минимальная скорость, которую необходимо сообщить находящемуся вблизи поверхности Земли телу, чтобы оно могло преодолеть гравитационное притяжение Земли и Солнца и покинуть пределы Солнечной системы^[1][2].

При старте с Земли, наилучшим образом используя осевое вращение (0.5 км/с) и орбитальное движение планеты (29,8 км/с), космический аппарат может достичь третьей космической скорости уже при 16,6 км/с^[2] относительно Земли. Для исключения влияния атмосферного сопротивления предполагается, что космический аппарат приобретает эту скорость за пределами атмосферы Земли. Наиболее энергетически выгодный старт для достижения третьей космической скорости должен осуществляться вблизи экватора, движение объекта должно быть сонаправлено осевому вращению Земли и орбитальному движению Земли вокруг Солнца. При этом скорость движения аппарата относительно Солнца составит 29.8 + 16.6 + 0.5 = 46.9 км/сек.

Траектория аппарата, достигшего третьей космической скорости, будет частью ветви параболы, а скорость относительно Солнца будет асимптотически стремиться к нулю.

На 2012 год ещё ни один космический аппарат не покидал окрестностей Земли с третьей космической скоростью. Наибольшей скоростью покидания Земли обладал КА Новые горизонты — 16.21 км/сек, но за счёт гравитационного маневра у Юпитера, он покинет Солнечную систему со скоростью около 13 км/сек после окончания основной части своей миссии. Аналогичным образом ускорялись и другие КА, уже покинувшие Солнечную систему (Вояджер-1 Вояджер-2, Пионер-10 и Пионер-11). Все они покидали окрестности Земли со скоростями, существенно меньшими третьей космической.

Вычисление

Для расчёта третьей космической скорости можно воспользоваться следующей формулой^[3]:

где v₃ — третья космическая скорость, а v₁ и v₂ — первая для Солнца и вторая для планеты космические скорости соответственно.

Примечания

1. ↑ Космические скорости
2. ↑ ^{1 2} Из Большой Советской Энциклопедии
3. ↑ Галузо И. В. Астрономия : учеб. пособие для 11-го кл. общеобразоват. учреждений с рус. яз. обучения / И. В. Галузо, В. А. Голубев, А. А. Шимбалёв. — 2-е изд., пересмотр. — Минск: Нар. асвета, 2009. — С. 70. — ISBN 978-985-03-1083-5.

См. также

Примечания

Ссылки

dic.academic.ru

Третья космическая скорость — Википедия

Материал из Википедии — свободной энциклопедии

Тре́тья косми́ческая ско́рость — минимальная скорость, которую необходимо придать находящемуся вблизи поверхности Земли телу, чтобы оно могло преодолеть гравитационное притяжение Земли и Солнца и покинуть пределы Солнечной системы^[1].

Вычисление

Для того, чтобы покинуть пределы Солнечной системы с орбиты Земли, ракета массой m{\displaystyle m} должна обладать скоростью относительно Солнца vC{\displaystyle v_{C}}, определяемой законом сохранения энергии

mvC22=GmMCRZC,{\displaystyle {\frac {mv_{C}^{2}}{2}}=G{\frac {mM_{C}}{R_{ZC}}},}

где MC{\displaystyle M_{C}} — масса Солнца, RZC{\displaystyle R_{ZC}} — радиус земной орбиты. Отсюда требуемая скорость ракеты относительно Солнца

vC=2GMCRZC.{\displaystyle v_{C}={\sqrt {\frac {2GM_{C}}{R_{ZC}}}}.}

Ракета вследствие движения вместе с Землей по орбите вокруг Солнца уже обладает скоростью вращения Земли вокруг Солнца, которую можно найти, применив второй закон Ньютона:

GMCmRZC2=mvZ2RZC,{\displaystyle G{\frac {M_{C}m}{R_{ZC}^{2}}}={\frac {mv_{Z}^{2}}{R_{ZC}}},}

откуда

vZ=GMCRZC.{\displaystyle v_{Z}={\sqrt {\frac {GM_{C}}{R_{ZC}}}}.}

Следовательно, при разгоне ракеты в направлении вектора скорости движения Земли по её орбите вокруг Солнца скорость космической ракеты vRZ{\displaystyle v_{RZ}} относительно Земли для выхода за пределы Солнечной системы должна быть равна

vRZ=vC−vZ=vZ(2−1).{\displaystyle v_{RZ}=v_{C}-v_{Z}=v_{Z}({\sqrt {2}}-1).}

Для того, чтобы удалить корабль из поля тяготения Земли, ему надо сообщить вторую космическую скорость

v2=2GMZRZ.{\displaystyle v_{2}={\sqrt {\frac {2GM_{Z}}{R_{Z}}}}.}

Следовательно, кинетическая энергия Ek{\displaystyle E_{k}}, которую надо сообщить космическому кораблю для того, чтобы он покинул Солнечную систему, складывается из кинетической энергии E2{\displaystyle E_{2}}, необходимой для того, чтобы покинуть поле тяготения Земли и кинетической энергии ERZ{\displaystyle E_{RZ}}, необходимой для того, чтобы он с орбиты Земли покинул поле тяготения Солнца

mv322=mv222+mvRZ22,{\displaystyle {\frac {mv_{3}^{2}}{2}}={\frac {mv_{2}^{2}}{2}}+{\frac {mv_{RZ}^{2}}{2}},}

откуда v3=v22+vRZ2{\displaystyle v_{3}={\sqrt {v_{2}^{2}+v_{RZ}^{2}}}}^[2].

Отсюда приходим к формуле^[3]:

v3=(2−1)2vZ2+v22,{\displaystyle v_{3}={\sqrt {({\sqrt {2}}-1)^{2}v_{Z}^{2}+v_{2}^{2}}},}

где vZ{\displaystyle v_{Z}} — орбитальная скорость планеты, v2{\displaystyle v_{2}} — вторая космическая скорость для планеты.

Подставляя численные значения (для Земли vZ{\displaystyle v_{Z}} = 29,783 км/с, v2{\displaystyle v_{2}} = 11,182 км/с), найдём

v3≈{\displaystyle v_{3}\approx } 16,650 км/с.

Практическое достижение

При старте с Земли, наилучшим образом используя осевое вращение (≈0,5 км/с) и орбитальное движение планеты (≈29,8 км/с), космический аппарат может достичь третьей космической скорости уже при ~16,6 км/с^[1] относительно Земли. Для исключения влияния атмосферного сопротивления предполагается, что космический аппарат приобретает эту скорость за пределами атмосферы Земли. Наиболее энергетически выгодный старт для достижения третьей космической скорости должен осуществляться вблизи экватора, движение объекта должно быть сонаправлено осевому вращению Земли и орбитальному движению Земли вокруг Солнца. При этом скорость движения аппарата относительно Солнца составит

29,8 + 16,6 + 0,5 = 46,9 км/с.

Траектория аппарата, достигшего третьей космической скорости, будет частью ветви параболы, а скорость относительно Солнца будет асимптотически стремиться к нулю.

На начало 2015 г. ни один космический аппарат не покидал окрестностей Земли с третьей космической скоростью. Наибольшей скоростью покидания Земли обладал КА Новые горизонты; эта скорость составила 16,26 км/с^[4] (гелиоцентрическая скорость 45 км/с), что меньше третьей космической на 0.34 км/с. Но за счёт гравитационного манёвра у Юпитера в 2007 году он ещё прибавил 4 км/c, что позволит ему в будущем уверенно покинуть гелиосферу. На момент окончания основной части своей миссии (исследование Плутона) «Новые горизонты» удалялись от Солнца с гелиоцентрической скоростью около 14 км/с ^{[источник не указан 1427 дней]}. Аналогичным образом ускорялись и другие КА, уже покинувшие гелиосферу (Вояджер-1, Вояджер-2, Пионер-10 и Пионер-11). Все они покидали окрестности Земли со скоростями, существенно меньшими третьей космической.

Примечания

1. ↑ ^{1 2} Третья космическая скорость // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
2. ↑ Кабардин О. Ф., Орлов В. А. Пономарева А. В. Факультативный курс физики. 8 класс. — М.: Просвещение, 1985 — с. 178
3. ↑ Галузо И. В. Астрономия : учеб. пособие для 11-го кл. общеобразоват. учреждений с рус. яз. обучения / И. В. Галузо, В. А. Голубев, А. А. Шимбалёв. — 2-е изд., пересмотр. — Минск: Нар. асвета, 2009. — С. 70. — ISBN 978-985-03-1083-5.
4. ↑ New Horizons Mission to Pluto — Windows to the Universe

См. также

wikipedia.green

Третья космическая скорость

   Третья космическая скорость — минимальная скорость, которую необходимо придать находящемуся вблизи поверхности Земли телу, чтобы оно могло преодолеть гравитационное притяжение Земли и Солнца и покинуть пределы Солнечной системы.

где v₃ — третья космическая скорость, а v₁ и v₂ — первая для Солнца и вторая для планеты космические скорости соответственно.

Полезная информация о третьей космической скорости:

   У поверхности Земли третья космическая скорость равна 16,7 км/с.

   При начальной скорости больше 7,9 км/с, но меньше 11,2 км/с космический аппарат движется вокруг Земли по криволинейной траектории — эллипсу. Чем больше начальная скорость, тем все более вытянут эллипс.

   При достижении некоторого значения скорости, называемого второй космической скоростью, эллипс превращается в параболу и космический корабль уходит от Земли безвозвратно. У поверхности Земли вторая космическая скорость равна 11,2 км/с. При скорости более второй космической тело движется по гиперболической траектории.

   При старте с Земли, наилучшим образом используя осевое вращение (≈0,5 км/с) и орбитальное движение планеты (≈29,8 км/с), космический аппарат может достичь третьей космической скорости уже при ~16,6 км/с относительно Земли. Для исключения влияния атмосферного сопротивления предполагается, что космический аппарат приобретает эту скорость за пределами атмосферы Земли. Наиболее энергетически выгодный старт для достижения третьей космической скорости должен осуществляться вблизи экватора, движение объекта должно быть сонаправлено осевому вращению Земли и орбитальному движению Земли вокруг Солнца. При этом скорость движения аппарата относительно Солнца составит 29,8 + 16,6 + 0,5 = 46,9 км/с.

   Траектория аппарата, достигшего третьей космической скорости, будет частью ветви параболы, а скорость относительно Солнца будет асимптотически стремиться к нулю.

   На 2012 год ещё ни один космический аппарат не покидал окрестностей Земли с третьей космической скоростью. Наибольшей скоростью покидания Земли обладал космический аппарат Новые горизонты — 16,21 км/с, но за счёт гравитационного маневра у Юпитера, он покинет Солнечную систему со скоростью около 30 км/с после окончания основной части своей миссии. Аналогичным образом ускорялись и другие космические аппараты, уже покинувшие Солнечную систему (Вояджер-1, Вояджер-2, Пионер-10 и Пионер-11). Все они покидали окрестности Земли со скоростями, существенно меньшими третьей космической.

Так же есть:

Первая космическая скорость: 

Вторая космическая скорость :   

Обозначения:

 — Первая космическая скорость

 — Вторая космическая скорость

 — Гравитационная постоянная

 — Масса Земли

 — Радиус Земли

 — Высота тела над поверхностью Земли

g — Ускорение свободного падения у поверхности Земли

infofiz.ru

Третья космическая скорость — это… Что такое Третья космическая скорость?



Третья космическая скорость

        наименьшая скорость (начальная), которую нужно сообщить телу у поверхности Земли, чтобы оно, преодолев действие земного притяжения, а затем действие притяжения Солнца, навсегда покинуло бы пределы Солнечной системы. Т.к. с. равна примерно 16,6 км/сек (при запуске на высоте 200 км над земной поверхностью). Т. к. с. определяется из условия, что тело, достигнув границы сферы действия тяготения (См. Сфера действия тяготения) Земли, имеет параболическую скорость (См. Параболическая скорость) относительно Солнца. Поскольку параболическая скорость на расстоянии земной орбиты равна 42,10 км/сек, минимальная скорость, которую должно иметь тело на границе сферы действия тяготения Земли, составляет 12,33 км/сек (направление скорости должно совпадать с направлением скорости орбитального движения Земли, равного в среднем 29,77 км/сек). См. Космические скорости.

Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.

• Третья конференция РСДРП
• Третья революция

Смотреть что такое «Третья космическая скорость» в других словарях:

• ТРЕТЬЯ КОСМИЧЕСКАЯ СКОРОСТЬ — скорость V3, при превышении которой космический аппарат, запускаемый с Земли, может, преодолев притяжение Земли и Солнца, уйти в межзвездное пространство; V3=16,67 км/с …   Большой Энциклопедический словарь

• ТРЕТЬЯ КОСМИЧЕСКАЯ СКОРОСТЬ — см. Космические скорости. Физическая энциклопедия. В 5 ти томах. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988 …   Физическая энциклопедия

• Третья космическая скорость — Третья космическая скорость  минимальная скорость, которую необходимо сообщить находящемуся вблизи поверхности Земли телу, чтобы оно могло преодолеть гравитационное притяжение Земли и Солнца и покинуть пределы Солнечной системы[1][2]. При… …   Википедия

• третья космическая скорость — минимальная скорость, которую нужно сообщить телу (например, космическому аппарату) вблизи поверхности Земли, чтобы оно могло, преодолев притяжение Земли и Солнца, навсегда покинуть Солнечную систему. Третья космическая скорость равна… …   Энциклопедический словарь

• ТРЕТЬЯ КОСМИЧЕСКАЯ СКОРОСТЬ — миним. скорость, к рую нужно сообщить телу (напр., космич. аппарату) вблизи поверхности Земли, чтобы оно могло, преодолев притяжение Земли и Солнца, навсегда покинуть Солнечную систему. Т. к. с. равна прибл. 16,6 км/с …   Естествознание. Энциклопедический словарь

• Третья космическая скорость — минимальная скорость, необходимая для того, чтобы космический летательный аппарат, запущенный с Земли, преодолел притяжение Солнечной системы и покинул ее. У поверхности Земли Т. к. с. v3 = 16,67 км/с …   Астрономический словарь

• ТРЕТЬЯ КОСМИЧЕСКАЯ СКОРОСТЬ — см. Космические скорости …   Большой энциклопедический политехнический словарь

• Космическая скорость — (первая v1, вторая v2, третья v3 и четвёртая v4)  это мин …   Википедия

• космическая скорость — наименьшая начальная скорость, которую необходимо сообщить телу, чтобы оно, начав движение вблизи небесного тела, преодолело его притяжение. Эта скорость зависит от массы небесного тела. Для планеты Земля различают три космические скорости.… …   Энциклопедия техники

• Вторая космическая скорость — Анализ первой и второй космической скорости по Исааку Ньютону. Снаряды A и B падают на Землю. Снаряд C выходит на круговую орбиту, D  на эллиптическую. Снаряд E улетает в открытый космос. Вторая космическая скорость (параболическая скорость …   Википедия

dic.academic.ru